基本概念##
刚体变换###
刚体变换也被称为欧氏变换,它在变化当中保持了向量的长度和相互之间的夹角大小,相当于我们把一个刚体原封不同的进行了移动或旋转,不改变它自身的样子。
点与向量的关系###
点和向量两者并不是等价的关系。向量$\overrightarrow{a}$是一个空间上的抽象概念,只有当我们将其与某个坐标系联系起来的时候,它就具象化为了坐标点。
$\begin{align}\overrightarrow{a} =
\begin{bmatrix} e_1&e_2&e_3 \end{bmatrix} \begin{bmatrix}a_1\\a_2\\a_3\end{bmatrix}
= a_1e_1 + a_2e_2 + a_3e_3 \end{align}$
这里$e_i$为列向量,代表了空间当中坐标系的一组基。
内积和外积###
- 内积
$$\begin{align}a \cdot b = a^Tb = \sum_{i=1}^{3}a_ib_i = |a||b|\cos<a,b> \end{align}$$
- 外积
$\begin{align}a \times b = \begin{bmatrix} i&j&k\\a_1&a_2&a_3\\b_1&b_2&b_3 \end{bmatrix} = \begin{bmatrix} a_2b_3 - a_3b_2\\a_3b_1 - a_1b_3\\a_1b_2 - a_2b_1\end{bmatrix} = \begin{bmatrix} 0&-a_3&a_2\\a_3&0&-a_1\\-a_2&-a_1&0 \end{bmatrix}b \triangleq a^ b \end{align}$
这里将$\overrightarrow{a}^$记为将向量$\overrightarrow a$变为反对称。外积的大小为$|a||b|\sin<a,b>$,是两个向量张成的四边形的有向面积。
欧拉角和旋转向量
假设我们有一个经过原点的旋转轴$\overrightarrow{u} = (x,y,z)^T$,我们希望将一个向量$\overrightarrow{v}$,以$\overrightarrow u$为旋转轴,旋转$\theta$度之后,变换到$\overrightarrow{v \prime }$

这时,我们就可以用一个旋转向量$\overrightarrow u$和角度$\theta$来表示一次旋转。由于以这种方式表示旋转需要四个自由度(向量三个,角度一个),而刻画一次选择只需要三个自由度(x,y,z)这就导致了冗余。所以,我们额外规定向量的模长为一,$|\overrightarrow u| = \sqrt{x^2 + y^2 + z^2} =1$。
欧拉角其实与旋转向量十分类似,但是却更加符合人们思考旋转的方式。欧拉角使用三个分离的转角,把一个旋转分解为三次绕不同轴的旋转。分解方式可以是多种多样的,但通常是分解为X轴,Y轴,Z轴。
- 绕物体Z轴旋转,得到偏航角
yaw - 绕旋转之后的Y轴旋转,得到俯仰角
pitch - 绕旋转之后的X轴旋转,得到滚转角
roll
那么一个三维向量[90,-60,80],就可以定义一次旋转了。但是使用欧拉角会出现万向锁(Gimbal Lock)的错误: 在俯仰角为$±90^°$的时候,第一次旋转与第三次旋转将会使用同一个轴,这使得系统丢失了一个自由度。

旋转矩阵##
在基本概念中提到,向量在刚体变化中的长度和相对夹角是不变的,利用这种不变性,我们可以得到:
$\begin{align}\begin{bmatrix}e_1&e_2&e_3\end{bmatrix}\begin{bmatrix}x_1\\y_1\\z_1\end{bmatrix} & = \begin{bmatrix}e_1^{‘}&e_2^{`}&e_3^{‘}\end{bmatrix}\begin{bmatrix}x_2\\y_2\\z_2\end{bmatrix} \\
\begin{bmatrix}x_1\\y_1\\z_1\end{bmatrix}
& = \underbrace{\begin{bmatrix}e_1^Te_1^{‘}&e_1^Te_2^{‘}&e_1^Te_3^{‘} \\ e_2^Te_1^{‘}&e_2^Te_2^{‘}&e_2^Te_3^{‘} \\
e_3^Te_1^{‘}&e_3^Te_2^{‘}&e_3^Te_3^{‘}\end{bmatrix}}_{R} \begin{bmatrix}x_2\\y_2\\z_2\end{bmatrix}
\end{align} $
我们将中间这个矩阵称为旋转矩阵R,它具有如下性质:
$\begin{align} SO(n) = \lbrace R \in \mathbb R^{n \times n} | RR^T = I, det(R) = 1 \rbrace \end{align} $
不管多少维的旋转矩阵,它都必须是正交矩阵,且满足公式6。同时满足$tr(R) = 2\cos\theta + 1$,$\theta$为旋转的角度。而旋转矩阵的特征值为$\lbrace e^{i\theta},e^{-i\theta},1\rbrace$。 可以根据$R\overrightarrow{n} = R$求解出旋转轴向量。
四元数##
复数基础
如果有两个复数$z_1 = a + bi,z_2 = c +di$,由分配率我们可得
$\begin{align}
z_1z_2 &= ac+adi+bci+bdi^2 \\
&= ac-bd+(bc+ad)i \\
&= \begin{bmatrix}a&-b\\b&a \end{bmatrix}\begin{bmatrix}c\\d \end{bmatrix}
\end{align}$
我们可以将$\begin{bmatrix}a&-b\\b&a \end{bmatrix}$ 看成一个二维旋转矩阵,将复平面上的向量$(c,d)$变换到$(ac-bd,bc+ad)$上。具体来说:
$\begin{align}
\begin{bmatrix}a&-b\\b&a \end{bmatrix} &= \sqrt{a^2 + b^2}\begin{bmatrix}\frac{a}{\sqrt{a^2 + b^2}}&\frac{-b}{\sqrt{a^2 + b^2}}\\\frac{b}{\sqrt{a^2 + b^2}}&\frac{a}{\sqrt{a^2 + b^2}} \end{bmatrix} \\
&=\sqrt{a^2 + b^2} \begin{bmatrix}\cos(\theta)&-\sin(\theta)\\\sin(\theta&\cos(\theta) \end{bmatrix}
\end{align}$
根据欧拉公式,我们可以进一步将二维旋转坐标写成极坐标的形式:
$\begin{align}
\begin{bmatrix}\cos(\theta)&-\sin(\theta)\\\sin(\theta&\cos(\theta) \end{bmatrix} = \cos(\theta) + i\sin(\theta) = e^{i\theta}
\end{align}$
注意这里的$\theta$是逆时针方向,同时多个二维旋转操作可以叠加,即若干个二维旋转矩阵相乘仍是一个旋转矩阵,而且与施加的次序无关。角度为多个旋转角之和
四元数定义与操作###
所有四元数$q \in \mathbb H$都可以写成如下形式:
$\begin{align} q = a + bi +cj +dk&(a,b,c,d \in \mathbb R)\end{align}$
其中:
$\begin{align}i^2=j^2=k^2=ijk=-1\end{align}$
通常可以简化表示为有序对形式:
$\begin{align}q=[s,\bf{v}]&&(\bf{v}=\begin{bmatrix}x\\y\\z\end{bmatrix},s,x,y,z \in \mathbb R) \end{align}$
如果一个四元数的$s==0$,即$q_0=[0,{\bf{v}}]$。那么我们就称$q_0$为纯四元数。两个纯四元数相乘:
$\begin{align}vu = [\bf -v \cdot u,v \times u]\end{align}$
四元数的加减法与复数保持一致,乘法可以总结为下表:
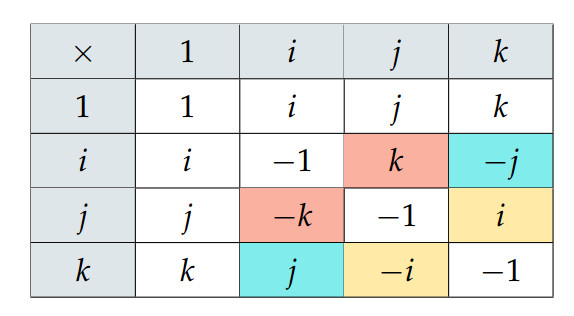
与复数一致,四元数的乘法也能写成矩阵乘向量的形式:
$\begin{align}q_1q_2 &= \begin{bmatrix}
a&-b&-c&-d\\
b&a&d&-c\\
c&-d&a&b\\
d&c&-b&a
\end{bmatrix}
\begin{bmatrix}
e\\f\\g\\h
\end{bmatrix}\\
&=(ae-(bf+cg+dh))+ \\
&(be+af+ch-dg)i+ \\
&(ce+ag+df-bh)j+ \\
&(de+ah+bg-cf)k \\
&=[ae-{\bf{u}} \cdot {\bf{v}}, a {\bf{u}}+e {\bf{v}}+{\bf{v}} \times \bf{u}]
\end{align}
$
其中:${\bf{v}} = \begin{bmatrix}b\\c\\d\end{bmatrix},{\bf{u}} = \begin{bmatrix}f\\g\\h\end{bmatrix}$
注意四元数并不满足交换律,即$q_1q_2 \neq q_2q_1$。这点与复数不一样。
四元数的逆和共轭
四元数共轭:$q^* = (s,-{\bf{v}})$
四元数的逆:$q^{-1} = \frac{q^*}{||q||^2}$
四元数的逆和共轭都满足交换律 : $q^*q = qq^*=||q||^2\quad;\quad q^{-1} =q^{-1}q=1$
单位四元数满足 : $q^{-1} = \frac{q^*}{||q||^2} = q^{*}$
四元数型3D旋转
任意向量$\bf v$沿着以单位向量定义的旋转轴$\bf u$旋转$\theta$度之后的$\bf v’$可以使用四元数乘法获得.用纯四元数$v = [0,{\bf v}]$表示三维空间中一个点,$\quad q = [\cos(\frac{1}{2}\theta),\sin(\frac{1}{2}\theta{\bf u})]$表示一次选择,那么:
$\begin{align}v’ = qvq^* = qvq^{-1}\end{align}$