<论文阅读>Canonical Surface Mapping via Geometric Cycle Consistency

Contribution
- 利用三维Template做为中介,弱化了实现稠密的,准确的多张图片对其所需的监督条件。
- 已有的图片到图片,图片到三维模型的映射关系的形成工作,不外乎依赖于人工手动标记对应点或者按照某些形变规则,将形变施加于图片A获得图片B,从而获得了A,B之间的对应关系。这些方法对于光照,角度等变量的鲁棒性较弱。
Method
- Preliminaries
作者利用两个参数将三维template平面化,$\overrightarrow u(u,v)$ 其中$u \in (0,1) v \in (0,1)$ 并且定义$ \phi(\overrightarrow u) $为恢复三维$(x,y,z)$的操作。
作者定义$\mathcal C \equiv f_\theta(I)$ 其中$f_\theta(I)$表示网络参数,作者将网络的预测行为抽象定义为$\mathcal C$
- Geometric Cycle Consistency Loss
$ \mathcal L_{cyc} = \sum_{p\in I_f} ||\overline p - p ||_{2}^{2} \quad;\quad \overline p = \pi(\phi(\mathcal {C}[p])) \tag{1}$
上面这个就是作者提出的一致性Loss,很好理解,就是像素$p$先经过网络映射在三维template上,接着投影回原图,两者之间的距离要尽可能小
- Incorporating Visibility Constraints
由于相机视角的原因,任何物体都会存在一个自遮挡的问题,而这个问题在预测图片稠密映射时就会产生一定的干扰。比方说,从正面看过去,一只鸟类的喙很有可能与其尾巴处于一条线上,所以当投影至二维像平面式,尾巴上某点就会被喙给遮挡。在这种情况下,如果映射关系预测网络将图片上的喙映射在三维template的尾巴上,最后投影回像平面计算$\mathcal L_{cyc} $的时候,依旧Loss会很小。所以作者就提出了:
$\mathcal L_{vis} = \sum_{p \in I_f}max(0,z_p - D_{\pi}[\overline p]) \tag{2}$
其中$D_{\pi}[\overline p]$是三维template在对应相机参数下的深度图。
- Mask Re-projection Loss & Multi-Hypothesis Pose Prediction
作者为了彻底摆脱对基准相机参数的需求,又新增了一个网络$g_{\theta^{‘}}$ 这个网络是用来预测相机,并且为了避免局部最小解(local minima),作者利用预测多个相机参数来达到这个目的。最后,作者使用一个约束来指导相机参数$\pi$的预测
$ \mathcal L_{mask} = ||f_{render}(S,\pi) - I_f||^2 \tag{3}$
其中$f_{render}$是在预测相机参数下,三维template投影至二维的Mask。 正如上面提到,作者会一次性预测多个相机参数,所以有${ (\pi_i,c_i)} \equiv g_{\theta’}(I) \quad i=1..8 $,其中$c_{i}$表示每个预测结果的概率是多少 。
最后,总的约束函数为:
$\mathcal L_{tot} = \mathcal L_{div}(g_{\theta’}(I)) + \sum_{i=1}^{N_c}c_i(\mathcal L_{cyc}^i + \mathcal L_{vis}^i + \mathcal L_{mask}^i) \tag{4}$
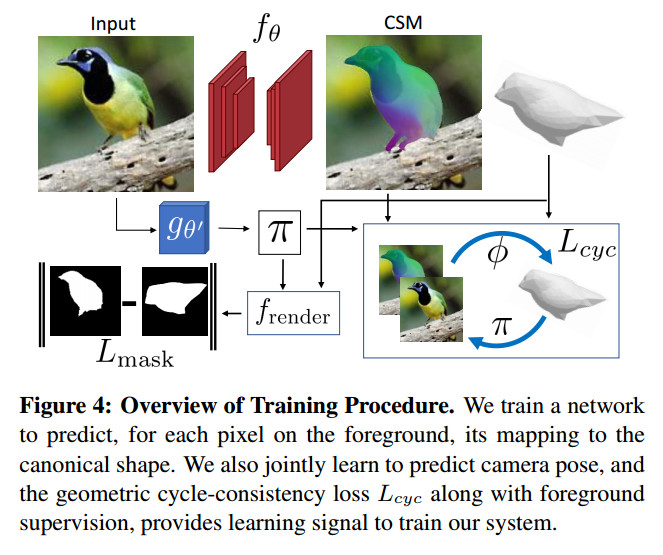
网络结构如图所示,对于2D-3D的映射关系预测,作者是利用一个U-Net结构(红色标注),输出为$B*4*H*W$的特征图,其中[:,:3,:,:]表示的是预测的三维坐标。[:,3,:,:]表示的是预测的mask。$H,W$分布代表输入图像的长和宽。$g_{\theta’}$表示相机参数预测网络,具体上,作者首先用ResNet18提取图片特征,接着送入FC层预测相关相机参数。作者在相机参数的预测网络上,有很多设定还是十分有趣的,有兴趣可以找来看下。
- 大致映射
之所以论文里提到approximate这个词呢,是因为,从代码上来看,$f_{\theta’}$的输出$BHW*4$中关于2D pixel to 3D vertex的映射并不一定是在template mesh上,对于网络输出的一对UV坐标(u,v),作者首先是找到离这对坐标最近的面片是哪一个,接着计算该点关于这个面片的重心坐标(barycentric coordinate),最后根据重心坐标和面片三个顶点的位置坐标,得到最终的3D坐标,同时也确保了这个坐标在template mesh上。可以想象一个四面体(A-BCD),网络预测的3D坐标可能是A点,那么作者就是找到A点在BCD上的对应点。
Experiments
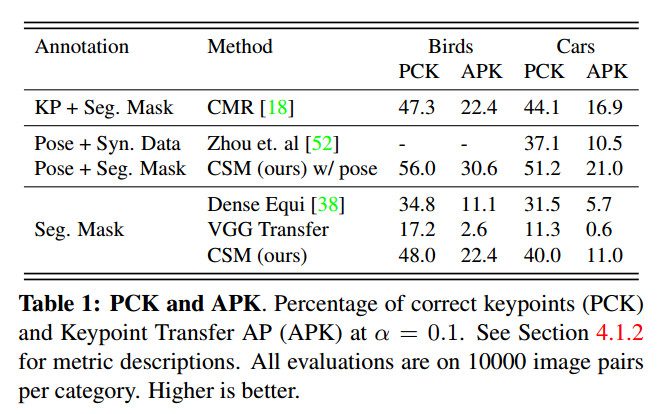

咋一看结果挺好,但是不知道作者为什么没有把CMR带基准相机参数的评测结果放出来,从消融实验的结果来看,在不利用预测相机参数的情况下,CSM结果并没有比不使用预测相机参数的CMR好太多,甚至在cars类别上的评分还低些