什么是旋转矩阵
旋转矩阵被用来在欧式空间进行旋转变换. 例如矩阵$R = \begin{bmatrix} \cos{\theta} & -\sin{\theta} \\ \sin{\theta} & \cos{\theta}\end{bmatrix}$,就是将二维平面上的某点逆时针旋转$\theta$度。
如果将向量(为了方便计算,这里将点表示为向量)和坐标系两者分离开,向量是独立于坐标系存在的。我们就可以将选择单独看作是坐标系的旋转,而旋转矩阵$R=[X_1, Y_1, Z_1]$中的每一列就表示原始坐标系的坐标轴在新坐标系下的投影长度。我们有两个坐标系$C_{new}$和$C_{old}$,且$X_{1} = \begin{bmatrix} \cos{\theta} & \sin{\theta} & 0 \end{bmatrix}^{T}$,则如下图所示:
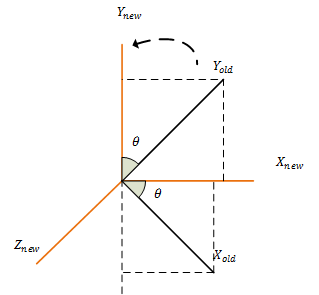
$X_{old}$在新坐标系下的投影分别是$X_{new}$:$\cos{\theta}$,$Y_{new}$:$\sin{\theta}$,$Z_{new}$:$0$,从而就得到了旋转矩阵的第一列$X_1$。其他列也是相同求解方法。
旋转矩阵的特性
根据WiKi上的定义:当且仅当方阵$R$满足$det(R)=1$,且$R^{-1} = R^{T}$,我们就称它为旋转矩阵。 而所有满足$det(R)=1$的正交矩阵所组成的集合被称为特殊正交群$SO(n)$(Sepcial Orthogonal Group), 而旋转就是属于$SO(3)$。而所有满足$det(R) = \pm1$的正交阵所形成的群被称为正交群$O(n)$
为什么旋转矩阵的行列式值必须为1
旋转是一种线性变换,而行列式就是线性变换的尺度因子,它会改变被变换向量的模长。如前边所讲,旋转操作是对坐标系的旋转操作,旋转是不会改变独立于坐标系客观存在的向量,我们所看到的“变化”仅仅是向量在某个坐标系下的表征方式,也就是我们常说的坐标。如果旋转矩阵的$det(R) \neq 1$,由于坐标系的基依旧是为单位向量,使得目标向量的模长发生了改变,那么这个操作就不能被称为旋转操作。
为什么旋转矩阵必须是正交矩阵
正交矩阵是行向量和列向量皆相互正交且为单位向量的方阵,满足$R^{-1} = R^{T}$。前边踢到,可以将旋转矩阵的每一列看作是原始坐标系上的坐标轴向量在目标坐标系下的投影。但其实我们稍微观察一下就可以发现,旋转向量的每一列其实还等于新坐标系下的坐标轴(表示方法是通过旧坐标系作为参考坐标系)。那么正是这个要求,使得其列与行向量必须正交。
旋转矩阵与其他旋转表征的转换
由旋转轴$u = \begin{bmatrix} u_x & u_y & u_z\end{bmatrix}$和旋转角度$\theta$可得绕任意旋转轴旋转任意角度的旋转矩阵为(具体推导过程可看:欧式空间的旋转表示(一)-轴角式:
$R = \begin{bmatrix}
\cos{\theta}+(1-\cos{\theta})u_x^2 & (1-\cos{\theta})u_xu_y-\sin\theta u_z & (1-\cos\theta)u_xu_z + \sin\theta u_y \\
(1-\cos\theta)u_yu_x + \sin\theta u_z & \cos\theta + (1-\cos\theta)u_y^2 & (1-\cos\theta)u_yu_z - \sin\theta u_x \\
(1-\cos\theta)u_zu_x - \sin\theta u_y & (1-\cos\theta)u_zu_y + \sin\theta u_x & \cos\theta + (1-\cos\theta)u_y^2
\end{bmatrix}$
旋转矩阵到轴角式
可以知道$tr(R) = 3\cos\theta + (1-\cos\theta)(u_x^2 + u_y^2 + u_z^2)$,由于旋转轴的模长为1,我们可得$\theta = \arccos{\frac{tr(R)-1}{2}}$。
观察旋转矩阵我们可以发现$\begin{bmatrix} R_{32} - R_{23} \\ R_{13} - R_{31} \\ R_{21} - R_{12}\end{bmatrix} = \begin{bmatrix} 2u_x\sin\theta \\ 2u_y\sin\theta \\ 2u_z\sin\theta \end{bmatrix}$,将所得向量归一化后即为旋转轴。然后便可使用右手螺旋定则(大拇指指向正方法,其余四指为正向旋转方向)。
由于旋转轴在选择过程中保持不变,我们也可以通过$Ru = R$来求解出旋转轴。
旋转矩阵到四元数
四元数$q = (w, x, y, z)$,其中$w = \cos{\frac{\theta}{2}};[x,y,z]^T=\sin{\frac{\theta}{2}}u^T$,u为旋转轴。根据上面的推导,我们可以知道$\cos\theta = \frac{tr(R)-1}{2}$,而$\cos\theta = 2\cos^2{\frac{\theta}{2}} - 1 = 2w^2-1$。所以我们可以知道$tr(R) = 4w^2 -1$。
而$(x,y,z)$也可用上面的公式得到$[x,y,z]^T = \frac{1}{4\cos\frac{\theta}{2}}[R_{32}-R_{23},R_{13} - R_{31},R_{21} - R_{12}]^T$