什么是欧拉角
欧拉角被用来描述一个物体绕某个坐标系旋转的角度,坐标系可以分解为三个相互正交的坐标轴构造。欧拉角的定义由三个部分组成:
顺规:欧拉角具有两大类的顺规表示方式:1)Proper Euler angles: (z-x-z, x-y-x, y-z-y, z-y-z, x-z-x, y-x-y); 2) Tait-Bryan angles:(x-y-z, y-z-x, z-x-y, x-z-y, z-y-x, y-x-z)。一般,我们也可以用yaw, pitch, roll来分别指代$z$轴,$y$轴, $x$轴的旋转。我们将其简称为$rpy$角
旋转角度:常用$(\gamma ,\beta ,\alpha)$来描述绕三个坐标轴旋转的角度, 若以ZYX顺规来解释,既先绕$z$轴旋转$\gamma$度,再绕$y$轴旋转$\beta$度,最后绕$x$轴旋转$\alpha$度。
内旋or外旋:根据每次旋转是绕旋转之后的轴旋转,还是固定轴旋转,我们将欧拉角分为内旋(intrisic roatation)和外旋(extrinsic rotation)。也有称内旋为动态旋转,绕物体坐标系旋转;将外旋称为静态旋转,绕世界坐标系旋转。事实上,如果将12种顺规中的一种的第一次旋转轴和第三次旋转轴互换顺序,那么可以使得外旋,内旋两者造成的姿态变化是等价的。比如外旋(z,y,x)就等价于内旋(x,y,z),证明如下:
根据题目可得如下定义:
$R_{外} = R(Z)R(Y)R(X)$ 和 $R_{内} = R(\alpha)R(\beta)R(\gamma)$。其中对于外旋来说,也是绕固定Z轴旋转$\gamma$度,绕固定Y轴旋转$\beta$度,绕固定X轴旋转$\alpha$度。
$R(\alpha) = R(X)$这是显然的,而$R(\beta)$可以写为$R(\beta) = R(\alpha)^{-1}R(Y)R(\alpha)$(可以用三支笔模拟一下)。同理我们可得$R(\gamma) = (R(\alpha)R(\beta))^{-1}R(Z)(R(\alpha)R(\beta))$。由此:
$R_{外} = R(\alpha)R(\beta)R(\gamma) \\
= R(\alpha)R(\beta)*(R(\alpha)R(\beta))^{-1}R(Z)(R(\alpha)R(\beta)) \\
= R(Z)(R(\alpha)R(\beta)) \\
= R(Z)(R(\alpha)R(\alpha)^{-1}R(Y)R(\alpha)) \\
= R(Z)R(Y)R(\alpha) \\
= R(Z)R(Y)R(X)$
我们可以从以上三个方面确定一次用欧拉角定义的旋转,当任意一个因素发生改变时,都可能形成另一种不一样的旋转。
什么是万向锁(Gimbal Lock)
假设我们的**顺规为zyx, 内旋,旋转角度为$(\gamma ,\beta ,\alpha)$**,当$\beta$为$\pm90$度时,就会产生万向锁。下面我们以内旋,顺规为(z,y,x)为例。
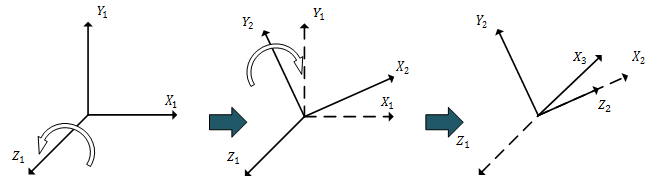
我们将起始地坐标轴定义为$(X_1, Y_1, Z_1)$首先我们绕$Z_1$轴旋转任意$\gamma$角,易得此时$X_1$轴和$Y_1$轴的方向已经发生了改变,记为$(X_2, Y_2, Z_1)$。我们再绕$Y_2$轴旋转90度,得到$(X_3, Y_2, Z_3)$。我们可以发现$X_3$轴与$Z_1$轴处以同一条水平线上。那么当我们按照顺规第三次绕$X_3$轴旋转时,本质上就是重复了第一次绕$Z_1$轴的旋转。此时就称发生了万向锁(Gimbal Lock)。
任何顺规都有可能发生万向锁,只要第二次旋转的角度为$\pm 90$度,就会发生万向锁。
视频在2分56秒的地方介绍了万向锁的本质,其实就是objects没有安装期望的轨迹运动到规定的位置。而不是真正意义上的“锁”住某个维度。或者可以这样理解(不确定,没经过数学推导),我们已知任何选择都可以分解为三次基本旋转矩阵,当我们规定顺规为(z,y,x)时,若分解得y的旋转度数为90度时,我们预想的$X$轴的旋转度数$\alpha$就变得”无效”了,(X轴此时抑郁第一次旋转绕的Z轴重复)。解决方法就是使用其他的顺规,从而规避的第二次旋转度数为$\pm 90$度
从矩阵角度看万向锁
当我们以顺规(z,y,z)对物体进行旋转时,我们可以将三个基本旋转矩阵写成一个$R = \begin{bmatrix} c_1c_2 & c_1s_2s_3 - c_3s_1 & s_1s_3 + c_1c_3s_2 \\ c_2s_1 & c_1c_3 + s_1s_2s_3 & c_3s_1s_2 - c_1s_3 \\ -s_2 & c_2s_3 & c_2c_3 \end{bmatrix} $
当第二次旋转角度为$\pm 90$度时,我们有$c2=0$和$s2=\pm 1$。于是矩阵就可以简化为$R = \begin{bmatrix} 0 & \pm c_1s_3 - c_3s_1 & s_1s_3 \pm c_1c_3 \\ 0 & c_1c_3 \pm s_1s_3 & \pm c_3s_1 - c_1s_3 \\ \pm 1 & 0 & 0 \end{bmatrix} = \begin{bmatrix} 0 & -\sin(\alpha \pm \gamma) & \cos(\alpha \pm \gamma) \\ 0 & \cos(\alpha \pm \gamma) & \sin(\alpha \pm \gamma) \\ \pm 1 & 0 & 0 \end{bmatrix} $
我们可以看出,当对$\alpha$进行选择操作时,就相当于在$\gamma$上施加了一个反方向的旋律,两者效果是等价的。这就是造成万向锁的原因,我们在三维空间中,只能进行两个维度的变化。
欧拉角与其他旋转表征的转换
欧拉角与旋转矩阵
由上边的定义可以,欧拉角可以分解为三个基本旋转的复合变换。所谓基本旋转是指以$X$轴,$Y$轴,$Z$轴。采用右手法则,设$\theta$为转角,我们可得三个基本旋转矩阵为:
$R_{X}(\theta) = \begin{bmatrix} 1 & 0 & 0 \\
0 & \cos{\theta} & -\sin{\theta} \\
0 & \sin{\theta} & \cos{\theta}
\end{bmatrix}$
$R_{Y}(\theta) = \begin{bmatrix} \cos{\theta} & 0 & \sin{\theta} \\
0 & 0 & 0 \\
-\sin{\theta} & 0 & \cos{\theta}
\end{bmatrix}$
$R_{Z}(\theta) = \begin{bmatrix} \cos{\theta} & -\sin{\theta} & 0 \\
\sin{\theta} & \cos{\theta} & 0 \\
0 & 0 & 1
\end{bmatrix}$
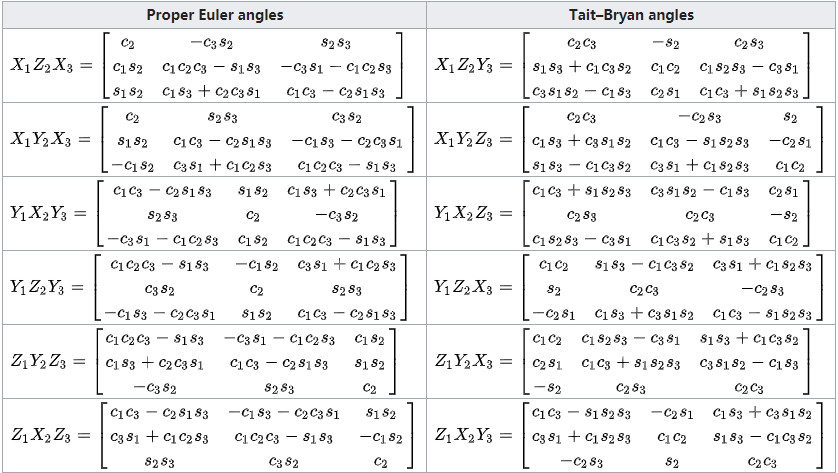
若顺规为(z,y,x),则$R = R_{Z}(\theta)R_{Y}(\theta)R_{X}(\theta)$。具体结果参照下图:
欧拉角与四元数
对于四元数$q = (w,x,y,z) = \cos{\theta} + \sin{\theta}x + \sin{\theta}y + \sin{\theta}z$。其中$\cos{\theta}$是表示旋转度数为$2\theta$,而$(x, y, z)$表明旋转轴。
而欧拉角转四元数就是,与欧拉角构造旋转矩阵一样,把三个基础旋转Elemental Rotation组合在一起。
$q(\gamma,\beta,\alpha) = q_{z}(\gamma)q_{y}(\beta)q_{x}(\alpha) \\
= \begin{bmatrix} \cos{\frac{\gamma}{2}} \\ 0 \\ 0 \\ \sin{\frac{\gamma}{2}} \end{bmatrix}
\begin{bmatrix} \cos{\frac{\beta}{2}} \\ 0 \\ \sin{\frac{\beta}{2}} \\ 0 \end{bmatrix}
\begin{bmatrix} \cos{\frac{\alpha}{2}} \\ \sin{\frac{\alpha}{2}} \\ 0 \\ 0 \end{bmatrix} \\
= \begin{bmatrix}
\cos{\frac{\gamma}{2}}\cos{\frac{\beta}{2}} \\ \sin{\frac{\gamma}{2}}\sin{\frac{\beta}{2}} \\
\cos{\frac{\gamma}{2}}\sin{\frac{\beta}{2}} \\ \sin{\frac{\gamma}{2}}\cos{\frac{\beta}{2}}
\end{bmatrix}
\begin{bmatrix} \cos{\frac{\alpha}{2}} \\ \sin{\frac{\alpha}{2}} \\ 0 \\ 0 \end{bmatrix} \\
= \begin{bmatrix}
\cos{\frac{\gamma}{2}}\cos{\frac{\beta}{2}}\cos{\frac{\alpha}{2}} - \sin{\frac{\gamma}{2}}\sin{\frac{\beta}{2}}\sin{\frac{\alpha}{2}} \\
\sin{\frac{\gamma}{2}}\sin{\frac{\beta}{2}}\cos{\frac{\alpha}{2}} + \cos{\frac{\gamma}{2}}\cos{\frac{\beta}{2}}\sin{\frac{\alpha}{2}} \\
\cos{\frac{\gamma}{2}}\sin{\frac{\beta}{2}}\cos{\frac{\alpha}{2}} - \sin{\frac{\gamma}{2}}\cos{\frac{\beta}{2}}\sin{\frac{\alpha}{2}} \\
\sin{\frac{\gamma}{2}}\cos{\frac{\beta}{2}}\cos{\frac{\alpha}{2}} - \cos{\frac{\gamma}{2}}\sin{\frac{\beta}{2}}\sin{\frac{\alpha}{2}}
\end{bmatrix}$