Diver

A coder in kindergarten

0%

拉普拉斯矩阵与拉普拉斯算子的关系

发表于 更新于
本文字数： 4.4k 阅读时长 ≈ 4 分钟
看过多篇论文都涉及到了利用拉普拉斯算子对重建网格模型进行光滑处理，但一直不清楚其背后的物理逻辑是什么，这里记录一下

目的

首先贴出一段利用拉普拉斯矩阵进行光滑处理的代码，根据Learning Category-Specific Mesh Reconstruction from Image Collections中的描述，拉普拉斯算子可以获得表面的平均曲率，通过最小化平均曲率，就可以使得表面变得光滑。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class LaplacianLoss(nn.Module):
    def __init__(self, vertex, faces, average=False):
        '''
			vertex: N*3
            faces: F*3
        '''
        super(LaplacianLoss, self).__init__()
        self.nv = vertex.size(0)
        self.nf = faces.size(0)
        self.average = average
        laplacian = np.zeros([self.nv, self.nv]).astype(np.float32)

        laplacian[faces[:, 0], faces[:, 1]] = -1
        laplacian[faces[:, 1], faces[:, 0]] = -1
        laplacian[faces[:, 1], faces[:, 2]] = -1
        laplacian[faces[:, 2], faces[:, 1]] = -1
        laplacian[faces[:, 2], faces[:, 0]] = -1
        laplacian[faces[:, 0], faces[:, 2]] = -1

        r, c = np.diag_indices(laplacian.shape[0])
        laplacian[r, c] = -laplacian.sum(1)

        for i in range(self.nv):
            laplacian[i, :] /= laplacian[i, i]

        self.register_buffer('laplacian', torch.from_numpy(laplacian))

    def forward(self, x):
        batch_size = x.size(0)
        x = torch.matmul(self.laplacian, x)
        dims = tuple(range(x.ndimension())[1:])
        x = x.pow(2).sum(dims)
        if self.average:
            return x.sum() / batch_size
        else:
            return x

Q：为什么拉普拉斯算子可以获得一个3D网格的平均曲率？

A: 图拉普拉斯矩阵，如果把它看作线性变换的话，它起的作用与数学分析中的拉普拉斯算子是一样的。也就是说拉普拉斯矩阵就是图上的拉普拉斯算子，或者说是离散的拉普拉斯算子。而拉普拉斯算子是用以获取连续可微函数的二阶微分（散度)。

拉普拉斯算子和拉普拉斯矩阵

符号定义

  • $f$是欧式空间中的二阶可微实函数，或从图的视角看作一组高维向量。
  • $\Delta$为拉普拉斯算子，求欧式空间的散度
  • $L$为拉普拉斯矩阵，求图空间的散度

理论推导

梯度（矢量） ：梯度 $\nabla$ 的本意是一个向量（矢量），表示某一函数在该点处的方向导数沿着该方向取得最大值，即函数在该方向处沿着该方向（此梯度方向）变化最快，变化率最大（为该梯度的模）。假设一个三元函数 $u=f(x,y,z)$ 在空间区域 $G$ 内具有一阶连续偏导数，点 $P(x,y,z) \in G$ ， 称向量

$\lbrace \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}, \frac{\partial f}{\partial z} \rbrace = \frac{\partial f}{\partial x} \overrightarrow{i} + \frac{\partial f}{\partial y} \overrightarrow{j} + \frac{\partial f}{\partial z} \overrightarrow{k} \tag{1}$

为函数$u=f(x,y,z)$在点$P$处的梯度，记为$gradf(x,y,z)$ 或 $\nabla f(x,y,z)$。其中： $\nabla = \frac{\partial}{\partial x} \overrightarrow{i} + \frac{\partial}{\partial y} \overrightarrow{j} + \frac{\partial}{\partial z} \overrightarrow{k}$ 被称为三维向量的微分算子。

散度（标量） 散度 $\nabla\cdot$（divergence）可用于表针空间中各点矢量场发散的强弱程度，物理上，散度的意义是场的有源性。当 $div(F)>0$ ，表示该点有散发通量的正源（发散源）；当 $div(F)<0$ 表示该点有吸收能量的负源（洞或汇）；当 $div(F)=0$ ，表示该点无源。

拉普拉斯算子： 拉普拉斯算子（Laplace Operator）是 $n$ 维欧几里得空间中的一个二阶微分算子，定义为梯度（ $\nabla f$ ）的散度（ $\nabla\cdot$ ）。 $\Delta f = \nabla^2f = \nabla \cdot \nabla f= div(gradf)$。 在笛卡尔坐标系下，拉普拉斯算子可以被表示为：

$\Delta f = \frac{\partial^2f}{\partial x^2} + \frac{\partial^2f}{\partial y^2} + \frac{\partial^2f}{\partial z^2} \tag{2}$

推广到$n$维空间中的形式为:

$\Delta = \sum \limits_{i} \frac{\partial^2f}{\partial x^2_i} \tag{3}$

如果将其推导到离散的形式下：

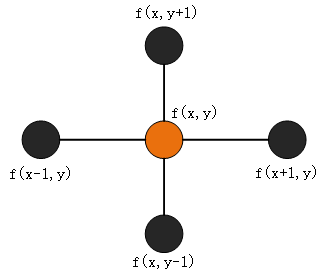
$\Delta f = \frac{\partial^2f}{\partial x^2} + \frac{\partial^2f}{\partial y^2} \\ =f(x+1, y) + f(x-1,y) - 2f(x,y) + f(x,y+1) - 2f(x,y) \\
=f(x+1, y) + f(x-1, y) + f(x, y+1) + f(x, y-1) - 4f(x,y) \tag{4}$

现在用散度的概念解读一下：

如果 $\Delta f = 0$ ，可以近似认为中心点 $f(x,y)$ 的势和其周围点的势是相等的， $f(x,y)$局部范围内不存在势差。所以该点无源
$\Delta f > 0$ ，可以近似认为中心点 $f(x,y)$ 的势低于周围点，可以想象成中心点如恒星一样发出能量，补给周围的点，所以该点是正源
$\Delta f < 0$ ,可以近似认为中心点 $f(x,y)$ 的势高于周围点，可以想象成中心点如吸引子一样在吸收能量，所以该点是负源
另一个角度，拉普拉斯算子计算了周围点与中心点的梯度差。当 $f(x,y)$ 受到扰动之后，其可能变为相邻的 $f(x+1,y), f(x-1,y), f(x,y+1), f(x,y-1)$ 之一，拉普拉斯算子得到的是对该点进行微小扰动后可能获得的总增益 （或者说是总变化）。

我们现在将这个结论推广到图： 假设具有 $N$ 个节点的图 $G$ ，此时以上定义的函数 $f$ 不再是二维，而是 $N$ 维向量： $f=(f_1,f_2,…,f_n)$ ，其中 $f_i$ 为函数 $f$ 在图中节点 $i$ 处的函数值(注意：在实际中这个‘函数值’通常不是一个标量，而是一个高维向量，表征某个特征信息)。类比于 $f(x,y)$ 在节点 $(x_i,y_i)$ 处的值。对 $i$ 节点进行扰动，它可能变为任意一个与它相邻的节点 $j \in N_i$ , $N_i$ 表示节点 $i$ 的一环邻域节点。

通过公式(4)，可以推广得到下面公式

$\Delta f_i = \sum \limits_{j \in N_i}W_{ij}(f_i - f_j) \tag{5}$

其中， $W_{ij}$表示的边的权重， $N_i$表示节点$i$的一环邻域。当$W_{ij} = 1$时，我们继续化简公式，可以得到：

$\Delta f_i = \sum \limits_{j \in N_i}W_{ij}(f_i - f_j) \\
=\sum \limits_{j \in N_i}W_{ij}f_i - \sum \limits_{j \in N_i}W_{ij}f_j \\
=d_if_i - \sum \limits_{j \in N_i}W_{ij}f_j \tag{6}$

我们把$d_i$记为节点$i$的度，那么我们可以得到对于$f=(f_1, f_2, \cdots,f_n)$的拉普拉斯矩阵为：

$\Delta f = Df - Wf \\
=(D-W)f \\
= \left(\begin{bmatrix} d_1 & 0 & \cdots & 0 & 0\\ 0 & d_2 & \cdots & 0 & 0\\ \vdots & 0 & \cdots & d_{n-1}& 0 \\ 0 & 0 & \cdots\ & 0 & d_{n}\end{bmatrix} - \begin{bmatrix} 1 & 0 & \cdots & 0 & 1 \\ 0 & 0 & \cdots & 1 & 0 \\ 1 & 1 & \cdots & 0 & 1 \\ 0 & 1 & \cdots & 0 & 1 \end{bmatrix}\right) f \\
= Lf \tag{7}$

其中，当边的权重$W_{ij}$均为1时，$D,W$分别为关于网（graph)的度矩阵和邻接矩阵。

总结

拉普拉斯矩阵$L$其实是离散化拉普拉斯算子的一种表示方式，通过这个方式，可以求得以图表示的，非规则结构的，点与点之间的二阶微分（某点曲率与该点关于函数的二阶导有关）。我们可以利用求得的曲率，来使平面变得光滑。

离散化拉普拉斯算子有多种表示形式，主要差别是符号，缩放因子上的差别。

公式(7)中的$W_{ij}$有不同的选择，比较常见的有常数1，度的倒数$\frac{1}{d_i}$, 余切权重 $\frac{\cot \alpha_{ij} + \cot \beta_{ij}}{2}$, $\alpha$和$\beta$为空间四边形$aibj$的相对角