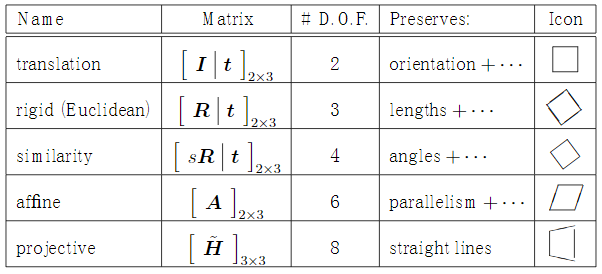
仿射变换:平移、旋转、放缩、剪切、反射
仿射变换包括如下所有变换,以及这些变换任意次序次数的组合:
平移(translation)和旋转(rotation)顾名思义,两者的组合称之为欧式变换(Euclidean transformation)或刚体变换(rigid transformation)
放缩(scaling)可进一步分为uniform scaling和non-uniform scaling,前者每个坐标轴放缩系数相同(各向同性),后者不同;如果放缩系数为负,则会叠加上反射(reflection)——reflection可以看成是特殊的scaling
刚体变换+uniform scaling 称之为,相似变换(similarity transformation),即平移+旋转+各向同性的放缩
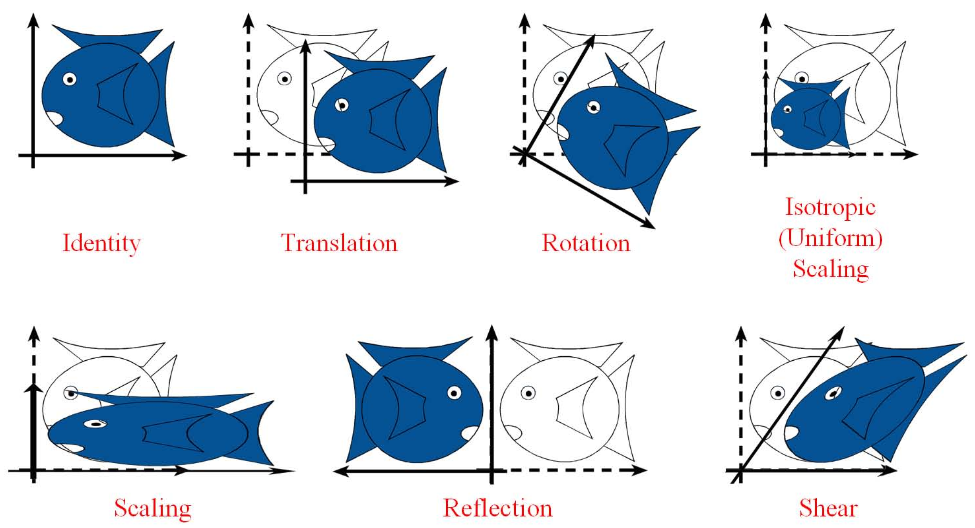
剪切变换(shear mapping)将所有点沿某一指定方向成比例地平移,语言描述不如上面图示直观。各种变换间的关系如下面的venn图所示
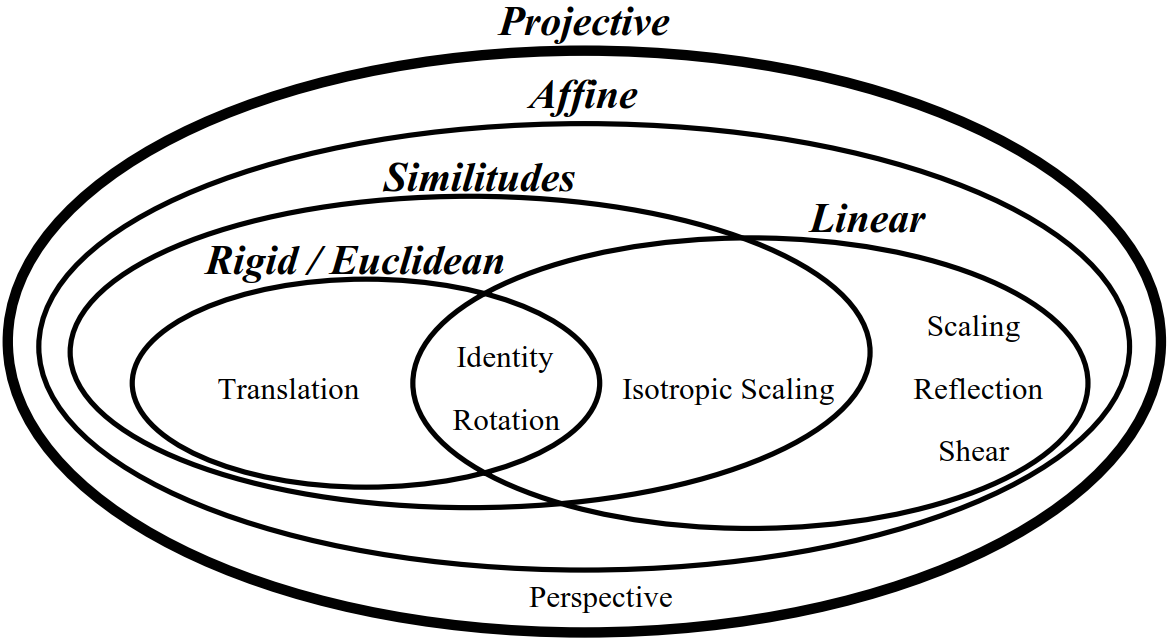
变换矩阵形式
没有平移或者平移量为0的所有仿射变换可以用如下变换矩阵描述:
$\left[ \begin{array}{l}{x’} \\ {y’}\end{array}\right]=\left[ \begin{array}{ll}{a} & {b} \\ {c} & {d}\end{array}\right] \left[ \begin{array}{l}{x} \\ {y}\end{array}\right]$
不同变换对应的a,b,c,d约束不同,排除了平移变换的所有仿射变换为线性变换(linear transformation),其涵盖的变换如上面的venn图所示,其特点是原点位置不变,多次线性变换的结果仍是线性变换。
为了涵盖平移,引入齐次坐标,在原有2维坐标的基础上,增广1个维度,如下所示:
$\left[ \begin{array}{l}{x^{\prime}} \\ {y^{\prime}} \\ {1}\end{array}\right] =\left[ \begin{array}{lll}{a} & {b} & {c}\\ {d} & {e} & {f} \end{array}\right] \left[ \begin{array}{l}{x} \\ {y} \\ {1}\end{array}\right]$
所以,仿射变换的变换矩阵统一用 $\left[ \begin{array}{lll}{a} & {b} & {c}\\ {d} & {e} & {f}\end{array}\right]$ 来描述,不同基础变换的$a,b,c,d,e,f$约束不同,因此,放射变换总共有6个自由度。如下所示:
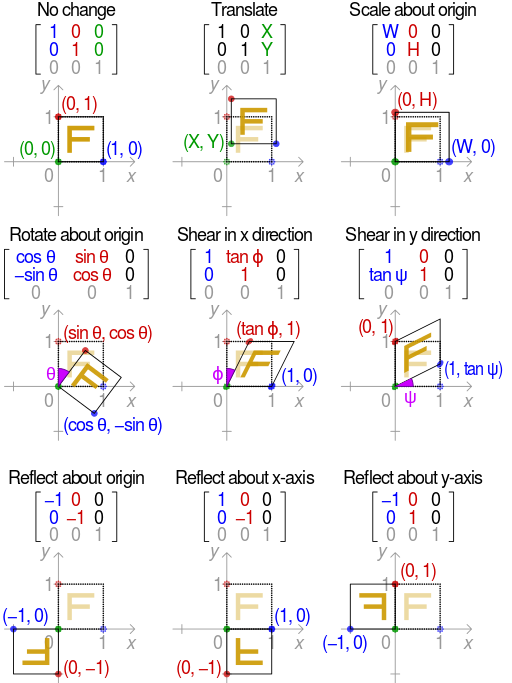
此外,旋转和平移相乘得到刚体变换的变换矩阵,如下,有3个自由度$(\theta, t_x, t_y)$,这里旋转方向为逆时针方向,因此与上图中的正负号不同,
$\left[ \begin{array}{ccc}{\cos (\theta)} & {-\sin (\theta)} & {t_{x}} \\ {\sin (\theta)} & {\cos (\theta)} & {t_{y}}\end{array}\right] \left[ \begin{array}{l}{x} \\ {y} \\ {1}\end{array}\right]=\left[ \begin{array}{c}{x^{\prime}} \\ {y^{\prime}} \\ {1}\end{array}\right]$
再乘上uniform scaling得到相似变换,有4个自由度($s, \theta, t_x, t_y$),如下:
$\left[ \begin{array}{ccc}{s\cos (\theta)} & {-s\sin (\theta)} & {t_{x}} \\ {s\sin (\theta)} & {s\cos (\theta)} & {t_{y}}\end{array}\right] \left[ \begin{array}{l}{x} \ {y} \\ {1}\end{array}\right]=\left[ \begin{array}{c}{x^{\prime}} \\ {y^{\prime}} \\ {1}\end{array}\right]$
变换矩阵的理解与记忆
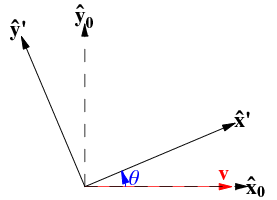
坐标系由坐标原点和基向量决定,坐标原点和基向量确定了,坐标系也就确定了。
对于坐标系中的位置$(x,y)$,其相对坐标原点在$[1,0]$方向上的投影为$x$,在$[0,1]$方向上的投影为$y$这里投影的意思是过$(x,y)$做坐标轴的平行线与坐标轴的交点到原点的距离,即$(x,y)$实际为:
$\left[ \begin{array}{l}{x} \\ {y}\end{array}\right] = x\left[ \begin{array}{l}{1} \\ {0}\end{array}\right] + y\left[ \begin{array}{l}{0} \\ {1}\end{array}\right] = \left[ \begin{array}{ll}{1} & {0} \\ {0} & {1}\end{array}\right] \left[ \begin{array}{l}{x} \\ {y}\end{array}\right]$
当坐标系变化,坐标系中的点也跟着变化,但点相对新坐标系($x′−y′坐标系$)的位置不变仍为$(x,y)$,以旋转变换为例,新坐标轴的基向量则变为$[cos(θ),sin(θ)]$和$[−sin(θ),cos(θ)]$,所以点变化到新位置为:
$\left[ \begin{array}{l}{x’} \\ {y’}\end{array}\right] = x\left[ \begin{array}{l}{\cos (\theta)} \\ { \sin (\theta)}\end{array}\right] + y\left[ \begin{array}{r}{- \sin (\theta)} \\ { \cos (\theta)}\end{array}\right] = \left[ \begin{array}{lr}{\cos (\theta)} & {-\sin (\theta)} \\ {\sin (\theta)} & {\cos (\theta)}\end{array}\right] \left[ \begin{array}{l}{x} \\ {y}\end{array}\right]$
所以,我们可以得出以下结论:
所有变换矩阵只需关注一点:坐标系的变化,即基向量和原点的变化, 在仿射变换矩阵$\left[ \begin{array}{lll}{a} & {b} & {c}\\ {d} & {e} & {f} \\ 0 & {0} & {1}\end{array}\right]$中, $\left[ \begin{array}{l}{a} \\ {d}\end{array}\right]$和$\left[ \begin{array}{l}{b} \\ {e}\end{array}\right]$为新的基向量,$\left[ \begin{array}{l}{c} \\ {f}\end{array}\right]$为新的坐标原点,先变化基向量,再变化坐标原点。
坐标系变化到哪里,坐标系中的所有点(这里表示的是相对点)也跟着做同样的变化。