Diver

A coder in kindergarten

0%

<论文阅读>(八)Occupancy Networks Learning 3D Reconstruction in Function Sapce

发表于 更新于 分类于 ，
本文字数： 3.5k 阅读时长 ≈ 3 分钟
作者通过将输入的图片映射到函数空间，然后在对于空间中采样若干点，对后通过marching cubes生成最后的重建结果。这种新的3维表示方法克服了已有方法（point cloud, voxel, mesh）的若干缺点。

<论文阅读>Occupancy Networks: Learning 3D Reconstruction in Function Sapce

论文链接

github

Contribution###

  • 作者在文中提出了一种新的3D表征方法，并证明了该表征方法可以用于高效的三维重建工作。
  • 作者提出了Multiresolution IsoSurface Extraction (MISE)用以从函数空间中恢复高精度的三维模型以较低的计算代价。

Backgroud###

作者认为主流的3D表征方法有着一下的不足：

Voxel###

Voxel是用规则的立方体来表示三维形状的。若想要提高Voxel的精度，所耗费的计算量是以三次方速度增长的，尽管有像Octree这种方法来减少计算量，但精度还是限制了$256^3$上边。

Point Cloud####

利用点来表示三维形状，与Voxel相比可以大幅度提高精度。但是由于缺少点与点之间的连接关系，就看上去就没有那么的直观。同时缩放性也较差。

Mesh###

通过增加点与点之间的连接关系，弥补了点云的不足。但是其拓扑结构不能改变，而如今基于Mesh表示三维重建工作，都是通过预测一个初始形状的deformation来进行三维重建，这就使得所预测的三维形状必须具有相同的拓扑结构（比方说一个空心圆圈和一个实心圆饼的拓扑结构就不一致）

Method

网络通过输入一个$p(x,y,z) \in \mathbb R^3$和一张图片或者点云或者体素$x \in \cal X$得到$p$点是否在物体内部的一个概率值probability of occupancy。

对于不同的类型的输入，作者使用不同的编码器来编码特征。

  • 图片 -> Resnet 18
  • 点云 -> PointNet encoder
  • 体素 -> 3D convolutional neural network

$f_{\theta}: \mathbb R^3 \times \cal X \rightarrow [0,1] \tag{1}$

从作者开源的代码来看，网络的decoder是一个输出维度为1的全连接层，我们将这个输出记为logits。在计算loss的时候，这个logits就与真实的occupancy value进行比较。

但是在评测IoU或者进行可视化的时候，就要用sigmoid(logits)来求得一个介于[0,1]之间的概率值，最后利用marching cubes进行可视化。

损失函数的定义也十分简单，就是一个交叉熵函数:

$\cal L_{\cal B}(\theta) = \frac{1}{|\cal B|}\sum\limits^{|\cal B|}\limits_{i=1}\sum\limits^{K}\limits_{j=1}\cal L(f_{\theta}(p_{ij},x_{i}),o_{ij}) \tag{2}$

其中$o_{ij}$表示真实的occupancy value

Occupancy Network Architecture

作者没有直接将encoder出来的特征向量c与输入的三维(x,y,z)坐标进行concat然后直接送入MLP进行映射，而是通过c来计算出batchnorm是denormalization所需要的scale和bias，以这种方式来影响最后pred-occupancy value的预测。作者在试验中也给出是否使用Conditional batch normalization的对比结果。

KL散度###

作者在文中提到:

Our 3D representation can also be used for learning probabilistic latent variable models

作者首先利用两个全连接来回归mean和log(std)（回归$\log(std)$是为了防止std为非正数）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
mean, logstd = encoder_latent(p, occ, c)
   # q_z 是一个正态分布
   q_z = dist.Normal(mean, torch.exp(logstd))
   # 随机采样一个z
   z = q_z.rsample()
   # 计算kl散度，使得编码mean, logstd的编码器尽量靠近正态分布，以保证张成空间的
   # 多样性。假设不加这个散度，为了让decoder每次生成的形状越来越好，那么每次送入
   # 的值都最好一致，那么logstd会逐渐变得很小，使得分布的标准差很小接近0。这样每
   # 次采样的结果z都近乎一致， 使得latent space并不能真的代表潜在空间。
   kl = dist.kl_divergence(q_z, p0_z).sum(dim=-1)
   
   # logits即为网络最终预测值，要与真实occupancy value进行比较。
   # 评估重建效果时，将sigmoid(logits)送入marching cubes进行重建 
   logits = decode(p, z, c)

由以上代码可知，最终重建的结果收到两个输入的影响,z 和 c。其中z是从表示c的分布中采样得到的，可以控制一定的形变。

可以看到，通过改变采样的z可以得到不同的形状。

Multiresolution IsoSurface Extraction (MISE)

假如我们已经学习到了一个函数空间$f_{\theta}$, 最直接的方式的采样的到具有$256^3$个点的grid, 然后得到每个点的pre-occupancy value，然后送入marching cube进行重建，但是这样大大限制了重建的精度。感觉上作者是借鉴的Octree的思想，逐步求解，最后达到预定分辨率。

Experiments###

Upper bound

作者首先评估了在函数空间中表示一个三维物体的可能性和其准确值，该准确值可以作为一个upper-bound来比较接下来的实验结果。由于是找到一个upper-bound，所以这个实验的训练个测试都是在训练集上进行的。实验步骤如下：

一： 将训练集中的所有图片（4746张）映射为一个长度为512维的特征向量，表征为latent space中的一个点，在训练过程中，图片->特征向量的映射关系保持不变。
二： 用一个decoder将512维的特征向量转换为一个1维的pred-occupancy value, 然后进行重建。

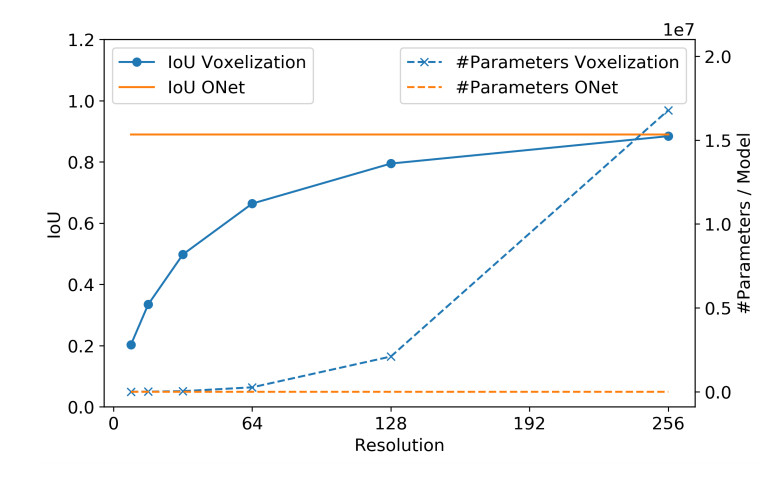
可以看到，本文所提出的表征方法，其重建精读（IoU）并不会随着分辨率的提高有太大的波动，始终保持在一个很高的水平(0.89)。同时，其网络参数也不会发生变化。反观基于Voxel的方法，虽然重建精度随着分辨率的提高有较大提升，但是其网络参数的增加量却是cubic。

Completion and Super-Resolution

正如前面提到的，网络Encoder的输入并不一定要是图片，还可以体素(Voxel), 点云(point cloud)。除了对图片所进行的单图重建任务（有3D监督）外，还对点云的补全和体素的超分都做了相应的实验。

Ablation Study

这里我们更关心的是第三行No CBN的对比结果。如果不使用Conditional Batch Normalization可以看到结果下降了比较大的幅度。具体到结构上的改变是，对于BN, 作者先是用一个全连接将输入的特征向量c映射为一个定好的长度(设为F1), 接着作者将待预测的点p(x,y,z)映射为相同的长度(F1) 然后两者相加后，在送入一维卷积+BN， 最后得到pred-occupancy value。

疑问###

Q:真实的occupancy value是如何取得的，在源码1和源码2可以看到评估和计算loss用到的网络输入确实是差一个sigmoid函数。但是真实的occ是如果求解的？

A: 在补充材料中，作者表示一个点真实的occupancy value的获取与其穿越的面片数有关。具体来讲，做一条与z轴平行且以p点为起点的直线，记为A, 若A穿过的面片数为偶数，则其在物体外部。反之，若A穿过面片数位奇数，则其在物体内部。

Q 论文中提到点的法向量可以通过求导得到，如何操作？

In addition, our approach also allows to efficiently extract normals for all vertices of our output mesh by simply backpropagating through the occupancy network.

Q 其实对于特征融合，像作者在Ablation Study这样，将两个没有很强关联的特征直接进行相加，然后卷积得到结果的情况是比较少见的。更多的是特征之间的Concat, 或者像GEOMetrics这篇文章一样，保留一部分。比较失望作者没有考虑到这个很明显的问题。