2019年12月18日更新:加入归并排序的两种链表版本:top-down, bottom-up。
2019年12月28日更新:加入桶排序算法
2020年3月20日更新:加入堆排序,计数排序,希尔排序
冒泡排序 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 //冒泡排序: 每次迭代最大的在最上方 int* sort(int* nums, int numsSize){ int tmp = 0; // 注意这里的起始值 for(int i =numsSize-1;i>0;i--){ //最大的值所放置的位置 for(int j = 0;j<i;j++){ // 比较的位置 if(nums[j] > nums[j+1]){ tmp = nums[j]; nums[j] = nums[j+1]; nums[j+1] = tmp; } } } return nums; }
时间复杂度:$O(n^2)$ 空间复杂度:$O(1)$ 稳定
选择排序 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 // 选择排序 找到最大或最小的值,放在最边的位置 int* sort(int* nums, int numsSize){ int minInd = 0; int tmp = 0; for(int i=0;i<numsSize-1;i++){ //最小值的位置 和 比较的位置 minInd = i; for(int j =i+1;j<numsSize;j++){ if(nums[minInd] > nums[j]){ minInd = j; } } // 交换 tmp = nums[i]; nums[i] = nums[minInd]; nums[minInd] = tmp; } return nums; }
时间复杂度:$O(n^2)$ 空间复杂度:$O(1)$ 不稳定
插入排序 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 // 插入排序 每次迭代,都与以排序好的数组进行比较,在排序好的数组中找到合适的位置。 int* sort(int* nums, int numsSize){ for(int i=0;i<numsSize;i++){ int tmp = nums[i]; int j =i; while(j>0 && tmp < nums[j-1]){ nums[j] = nums[j-1]; j=j-1; } nums[j] = tmp; } return nums; }
时间复杂度:$O(n^2)$ 空间复杂度:$O(1)$ 稳定
归并排序
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 // 归并排序 分治算法 void merge(int* nums, int start, int mid, int end){ // for(int i=start;i<=end;i++){ // printf("%d ",nums[i]); // } // printf("\n"); int p =start, q =mid+1; int* newNums = (int*)malloc(sizeof(int) * (end-start+1)); int k =0; for(int i = start;i<=end;i++){ // 检查第一部分是否完毕 if(p > mid) newNums[k++] = nums[q++]; else if(q > end) newNums[k++] = nums[p++]; else if(nums[p] < nums[q]) newNums[k++] = nums[p++]; else newNums[k++] = nums[q++]; } for(int p=0;p<k;p++){ nums[start++] = newNums[p]; } } void divide(int* nums, int start, int end){ if(start < end){ int mid = (start + end) / 2; divide(nums,start,mid); divide(nums, mid+1, end); merge(nums, start , mid ,end); } } int* sort(int* nums, int numsSize){ divide(nums, 0, numsSize-1); return nums; }
时间复杂度:$O(n\log_2{n})$ 空间复杂度:$O(n+log_2{n})$ 稳定
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 class Solution { public: ListNode* sortList(ListNode* head) { if(!head || !head->next) return head; /* 这里head->next是要给trick, 因为如果不加next的话,若子链长度为2,在 一次walk之后,fast指向nullptr,slow就指向最后一个元素,而下边有mid =slow->next = nullptr 所以就直接返回了,等于只有左半边链。而这时做半边脸仍然有两个元素,就会陷入循环,导致无法正常结束。 换句话说,如果不加next, 当子链长度为2时,就无法继续进行分治(分为左右两个长度为1的子链),使得程序无法结束。 而又由于我们使用递归,使得栈不断有新数据写入,最后就栈满溢出。 */ ListNode* slow = head; ListNode* fast = head->next; // 当fast走到低时,slow正好在中间 while(fast && fast->next){ fast = fast->next->next; slow = slow->next; } ListNode* mid = slow->next; // 将左,右两个子链断开 slow->next = nullptr; return merge(sortList(head), sortList(mid)); } private: // 两个子链排序,空间复杂度为常数 ListNode* merge(ListNode* l1, ListNode* l2){ ListNode dummy(0); ListNode* tail = &dummy; while(l1 && l2){ if(l1->val > l2->val) swap(l1,l2); tail->next = l1; l1 = l1->next; tail = tail->next; } if(l1) tail->next = l1; if(l2) tail->next = l2; return dummy.next; } };
时间复杂度:$O(log_2{n})$ 空间复杂度$(log_2{n})$ 稳定
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 class Solution { public: ListNode* sortList(ListNode* head) { if(!head || !head->next) return head; //由于我们采用bottom-up,所以需要知道整个链表的长度,作为大致范围的限制,但要求不算严格 int len = 0; ListNode* cur = head; // 获取长度 while(cur = cur->next) ++len; ListNode dummy(0); dummy.next = head; ListNode* l; ListNode* r; ListNode* tail; for(int n =1; n<len; n<<=1){ /* cur不能等于head, 因为head只是一个存储值得指针名,并不是代表 它在每次排序之后,都是头结点,可能在一次排序过后,head指针所 指的那个元素,就被放置在了最尾处,所以不能每次都将起始位置初始化为head. 这也是为什么要维护一个dummy结点,使dummy结点每次都指向真正的头节点。 */ // cur = head; cur = dummy.next; tail = &dummy; while(cur){ l = cur; r = split(l, n); cur = split(r, n); auto merged = merge(l, r); tail->next = merged.first; tail = merged.second; } } return dummy.next; } private: // 前n个元素一组,剩下的元素一组,返回剩下元素的head ListNode* split(ListNode* head, int n){ // 这里需要注意的是子链长度n是包括了头结点的长度 while(--n && head) head = head->next; ListNode* rest = head ? head->next : nullptr; if(head) head->next = nullptr; // 上面两行或换成下面易懂 // if(head){ // rest = head->next; // head->next = nullptr; // }else{ // rest = nullptr; // } return rest; } pair<ListNode*, ListNode*> merge(ListNode* l1, ListNode* l2){ ListNode dummy(0); ListNode* tail = &dummy; while( l1 && l2){ if(l1->val > l2->val) swap(l1,l2); tail->next = l1; l1 = l1->next; tail = tail->next; } tail->next = l1 ? l1 : l2; while( tail->next) tail = tail->next; return {dummy.next, tail}; } };
时间复杂度:$O(log_2{n})$ 空间复杂度:$O(1)$
首先对于Top-Down版本来讲,数组版本由于每次需要新建一个数组来对左右两部分子数组进行排序,所以相较于链表版本来说要多$O(n)$的空间复杂度。而对于Top-Down的版本,无论是数组还是链表,都比Bottom-up版本多了递归操作,所以空间复杂度要多$O(log_2{n})$。
快速排序## 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 int partition(int* nums, int start, int end) { int pivot = start; int l = pivot + 1; int r = end; int tmp = 0; // 等号是防止长度为2的子序列 while (l <= r) { while (l <= end && nums[l] <= nums[pivot]) { ++ l; } while (r >= start && nums[r] > nums[pivot]) { -- r; } if (l < r) { tmp = nums[l]; nums[l] = nums[r]; nums[r] = tmp; } }; // 这里由于pivot是取到最*左边*一个,要保证交换后,pivot左侧必须全部小于pivot,右侧必须全部大于pivot,就必须 // 与右指针所指元素进行交换(因为这时候右指针所指元素(记为i)小于pivot,交换之后,i还是在pivot*左边*,这就符合条件。 // 假设与左指针进行交换,那么由于做指针所指元素大于pivot,交换之后,在pivot左边就有一个大于pivot的元素,不符合条件。 tmp = nums[pivot]; nums[pivot] = nums[r]; nums[r] = tmp; pivot = r; return pivot; } void quick_sort(int* nums, int start, int end){ if(start < end){ int piv_pos = partition(nums, start, end); quick_sort(nums,start,piv_pos-1); // sorts the left side of pivot quick_sort(nums, piv_pos+1,end); } } int* sort(int* nums, int numsSize){ quick_sort(nums,0,numsSize-1); return nums; }
时间复杂度:$O(n\log_2{n})$ 空间复杂度:$O(1)$ 不稳定
桶排序## 桶排序(Bucket sort)或所谓的箱排序,是一个排序算法,工作的原理是将数组分到有限数量的桶里。每个桶再个别排序(有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排序)。桶排序是鸽巢排序的一种归纳结果。当要被排序的数组内的数值是均匀分配的时候,桶排序使用线性时间$\Theta (n)$。但桶排序并不是比较排序,他不受到$O(n\log_2 n)$下限的影响。具体步骤如下:
设置一个定量的数组当做空桶子
寻访序列,并且把每一个元素一个一个放到对应的桶子中
对每个不是空的桶子进行排序
从不是空的桶子里把项目再放回原来的序列中。
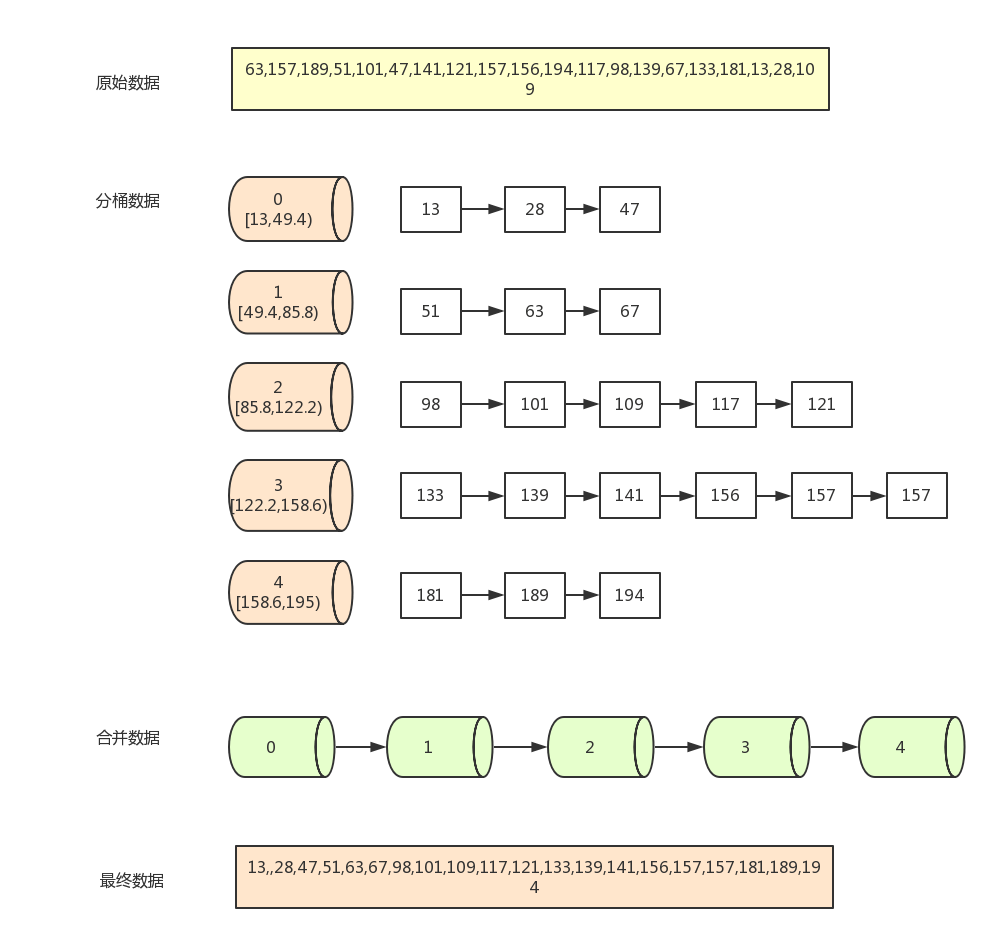
假设我们有一组长度为20的数据, 同时设定空桶子数量为5:
[63,157,189,51,101,47,141,121,157,156,194,117,98,139,67,133,181,13,28,109]
找到数组中的最大值194和最小值13,然后根据桶数为5,计算出每个桶中的数据范围为(194-13+1)/5=36.4
遍历原始数据,(以第一个数据63为例)先找到该数据对应的桶序列(63 - 13) / 36.4) =1,然后将该数据放入序列为1的桶中(从0开始算)
当向同一个序列的桶中第二次插入数据时,判断桶中已存在的数字与新插入的数字的大小,按从左到右,从小打大的顺序插入。如第一个桶已经有了63,再插入51,67后,桶中的排序为(51,63,67) 一般通过链表来存放桶中数据。
全部数据装桶完毕后,按序列,从小到大合并所有非空的桶(如0,1,2,3,4桶)
全部数据装桶完毕后,按序列,从小到大合并所有非空的桶(如0,1,2,3,4桶)
桶排序的时间复杂度主要受两个因素影响。
循环计算每个元素是属于哪个桶:O(n)
对每个桶内的元素进行排序,受不同排序算法的影响,最好情况为:$\sum \limits^{N} \limits_{i=1}O(n_i\log_2(n_i))$, $n_i$为每个桶内的元素数量。
可以看出,若每个桶内的数量均为1的话,则时间复杂度为$O(n)$
堆排序 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 #include<iostream> #include<vector> #include<string> using namespace std; void show(const vector<int>& nums,const string& describe){ cout << describe << ": "; for(int i : nums) cout << i << " "; cout << endl; } // 自底向上建堆 void AdjustBottom2Up(vector<int>& nums){ int len = nums.size(); for(int i=len-1; i>0; i = (i-1)/2){ if(nums[i] > nums[(i-1)/2]){ swap(nums[i], nums[(i-1)/2]); } } return; } /* 自顶向下调整时,注意要判断有单个结点或双个结点的情况 */ void AdjustTop2Down(vector<int>& nums, int i){ int len = nums.size()-1; // show(nums, "Adjust"); while(i<=(len-1)/2){ int nextI = 2*i+1; if(2*i+2 <= len){ nextI = nums[2*i+1] > nums[2*i+2] ? nextI : (2*i+2); } if(nums[nextI] > nums[i]){ swap(nums[nextI], nums[i]); i = nextI; }else{ break; } // show(nums, "Adjust"); } return; } void Insert(const int i, vector<int>& nums){ nums.push_back(i); show(nums, "Before Insert"); AdjustBottom2Up(nums); show(nums, "After Insert"); } void Pop(vector<int>& nums){ int len = nums.size(); // show(nums, "Debug"); swap(nums[0], nums.back()); // show(nums, "Debug"); nums.pop_back(); // show(nums, "Debug"); AdjustTop2Down(nums, 0); // show(nums, "Debug"); } vector<int> BuildMaxHeapOut(const vector<int>& nums){ int len = nums.size(); vector<int> res; for(int i=0; i<len; i++){ Insert(nums[i], res); } return res; } void BuildMaxHeapIn(vector<int>& nums){ int len = nums.size(); for(int i=(len-1)/2; i>=0; i--){ AdjustTop2Down(nums, i); } } int main(){ vector<int> nums{5,6,3,1,7,5,7,4,12,13,11,20,5,32,18,22}; // Out-Place 操作 show(nums,"Before BuildMaxHeap"); auto res = BuildMaxHeapOut(nums); show(res, "After BuildMaxHeap"); cout << "===================Insert==================\n" << endl; show(res, "Before Insert"); Insert(15, res); show(res, "After Insert"); show(res, "Before Insert"); Insert(19, res); show(res, "After Insert"); cout << "===================Pop======================\n" << endl; for(int i=0; i<10; i++){ show(res, "Before Pop"); Pop(res); show(res, "After Pop"); } cout << endl; cout << "In-Place Sort" << endl; // In-Place 操作 show(nums,"Before BuildMaxHeap"); BuildMaxHeapIn(nums); show(nums, "After BuildMaxHeap"); // 32 22 20 12 13 5 18 4 6 7 11 5 5 7 3 1 cout << "===================Insert==================\n" << endl; show(nums, "Before Insert"); Insert(15, nums); show(nums, "After Insert"); show(nums, "Before Insert"); Insert(19, nums); show(nums, "After Insert"); cout << "===================Pop======================\n" << endl; for(int i=0; i<10; i++){ show(nums, "Before Pop"); Pop(nums); show(nums, "After Pop"); } return 0; }
堆可以看作是一个完全二叉数,为了方便比较,用数组方式存储。
堆的构建有两种,一个是In-Place的操作,就是不占用额外的空间;另外一种是将建堆看成是循环插入,是一中Out-Place的插入方式,每次插入最后一个位置。第一种方法需要从第$(n-1)/2$个元素开始,遍历到第$0$个元素。在每次遍历的时候,都需要从当前位置,往下(TOP-Down)判断当前子堆是否合法。第二种方法就是往上(Bottom-Up)的方法,将新插入元素放在堆的最后一位上,然后跟父结点进行判断。
堆删除时,需要将第一个元素与最后一个元素进行交换,然后弹出最后一个元素。接着从第一个元素开始,自顶向下调整堆(这与第一种建堆的方式一致)。
计数排序 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 #include <iostream> #include <vector> #include <algorithm> using namespace std; int main() { vector<int> nums{1,6,4,2,7,8,4,2,6,10}; int maxE=nums[0], minE=nums[0]; for(int i=0; i<nums.size(); i++){ maxE = max(nums[i], maxE); minE = min(nums[i], minE); } vector<int> cnt(maxE-minE+1,0); for(int i : nums){ cnt[i-minE]++; } for(int i=1; i<cnt.size(); i++){ cnt[i] += cnt[i-1]; } vector<int> res(nums.size(), 0); for(int i=nums.size()-1; i>=0; i--){ res[--cnt[nums[i]-minE]] = nums[i]; } for(int i : res) cout << i << " "; return 0; }
思想:如果比元素x小的元素个数有n个,则元素x排序后位置为n+1。
希尔排序 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 #include<iostream> #include<vector> #include<string> using namespace std; void show(const vector<int>& nums,const string& describe){ cout << describe << ": "; for(int i : nums) cout << i << " "; cout << endl; } void shellsort1(vector<int>& a, int n) { int i, j, gap; for (gap = n / 2; gap > 0; gap /= 2) //步长 for (i = 0; i < gap; i++) //直接插入排序 { for (j = i + gap; j < n; j += gap) if (a[j] < a[j - gap]) { int temp = a[j]; int k = j - gap; while (k >= 0 && a[k] > temp) { a[k + gap] = a[k]; k -= gap; } a[k + gap] = temp; } } } int main(){ vector<int> nums{3,5,2,7,6,5,8,9,11,2,31,21,15,17,20}; int n = nums.size(); shellsort1(nums, n); show(nums, "After Shell Sort: "); }
希尔排序的实质就是分组插入排序 ,该方法又称缩小增量排序。
该方法的基本思想是:先将整个待排元素序列分割成若干个子序列(由相隔某个“增量”的元素组成的)分别进行直接插入排序,然后依次缩减增量再进行排序,待整个序列中的元素基本有序(增量足够小)时,再对全体元素进行一次直接插入排序。因为直接插入排序在元素基本有序的情况下(接近最好情况),效率是很高的,因此希尔排序在时间效率上比前两种方法有较大提高。
基数排序 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 int maxbit(int data[], int n) //辅助函数,求数据的最大位数 { int maxData = data[0]; ///< 最大数 /// 先求出最大数,再求其位数,这样有原先依次每个数判断其位数,稍微优化点。 for (int i = 1; i < n; ++i) { if (maxData < data[i]) maxData = data[i]; } int d = 1; int p = 10; while (maxData >= p) { //p *= 10; // Maybe overflow maxData /= 10; ++d; } return d; } void radixsort(int data[], int n) //基数排序 { int d = maxbit(data, n); int *tmp = new int[n]; int *count = new int[10]; //计数器 int i, j, k; int radix = 1; for(i = 1; i <= d; i++) //进行d次排序 { for(j = 0; j < 10; j++) count[j] = 0; //每次分配前清空计数器 for(j = 0; j < n; j++) { k = (data[j] / radix) % 10; //统计每个桶中的记录数 count[k]++; } for(j = 1; j < 10; j++) count[j] = count[j - 1] + count[j]; //将tmp中的位置依次分配给每个桶 for(j = n - 1; j >= 0; j--) //将所有桶中记录依次收集到tmp中 { k = (data[j] / radix) % 10; tmp[count[k] - 1] = data[j]; count[k]--; } for(j = 0; j < n; j++) //将临时数组的内容复制到data中 data[j] = tmp[j]; radix = radix * 10; } delete []tmp; delete []count; }
基数排序时间复杂度为$O(nk)$,其中$n$为元素个数,$k$为元素的属性。如果是数字的话,就是数字的位数。