<论文阅读>End-to-end Recovery of Human Shape and Pose
Contribution
- 单图重建
- 利用SMPL进行重建,并且达到real-time效果
- 不要求每一个训练的image都要有其对应的3D ground truth
Method
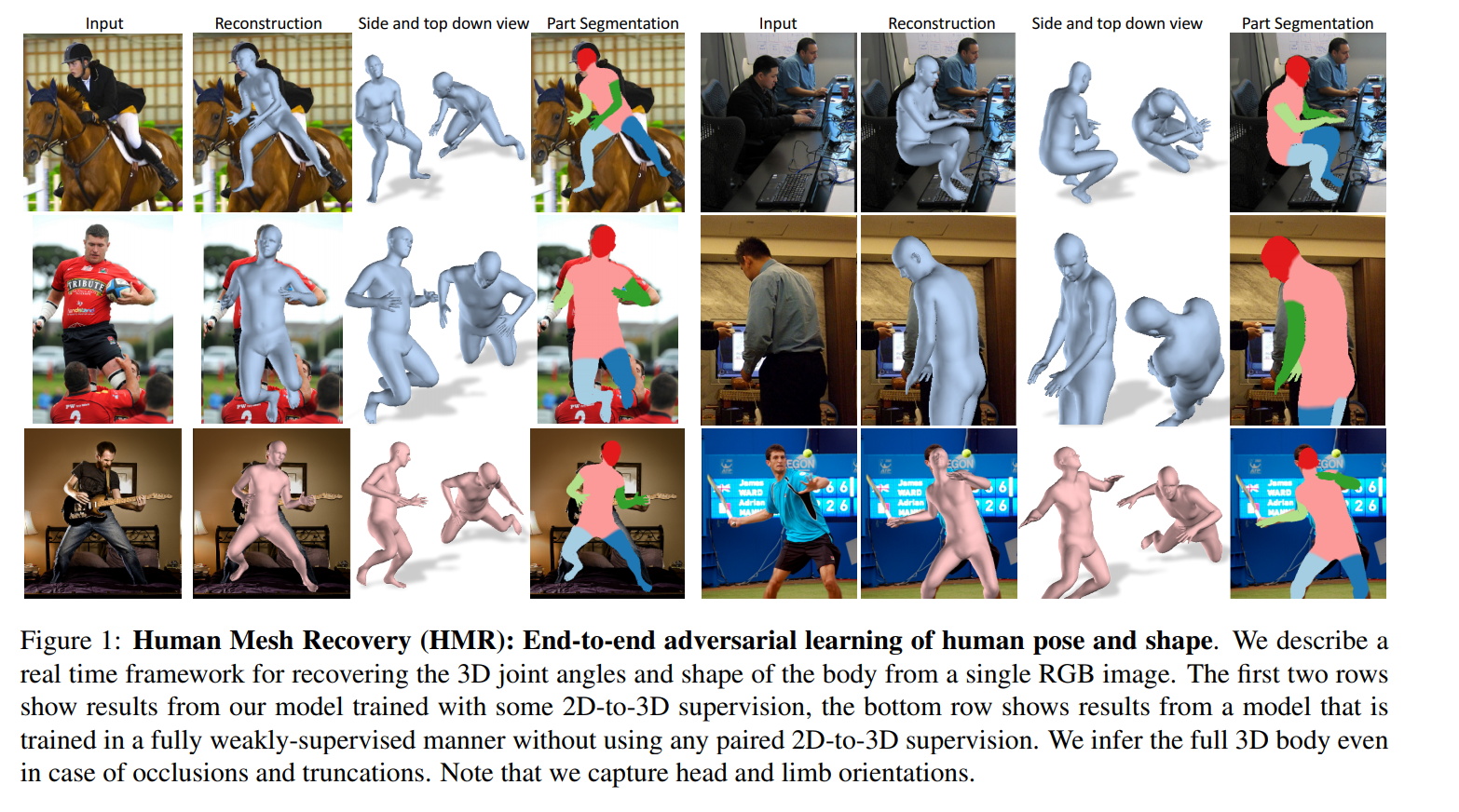
作者提出了一个end-to-end的网络来从单张RGB人像恢复其3D形状。作者利用已有的SMPL模型,SMPL模型可由3D relative joint rotation和Shape 来刻画一个人的3D shape。作者认为在以往的人体建模工作当中,有3D joint location来估计一个完整的3D shape 是不鲁棒的。原因有二:1、3D joint location alone do not constrain the full DoF at each joint. DoF意思就是景深,这个跟相机的参数有关。对这个参数的估计错误,可能会导致所估计的3D shape在图像中的显示位置有区别(我自己想的,不一定正确)2、Joints are sparse, whereas the human body is defined by a surface in 3D space. 这个就是Joints的点数过少,不足以约束一个完整的3D human shape。
作者还解决了两个在重建工作的问题。其一就是缺少3D ground-truth数据,同时,已有的3D ground-truth绝大部分是在实验室环境下采集的,其对in the wild的2D图像泛化性很差。其二就是单视角情况下2D-3D mapping的问题,不同的3D shape存在对应一张相同的2D图片,在这些3D shape中,存在一些不正常的shape(may not be anthropometrically reasonable)
网络训练
- 网络结构
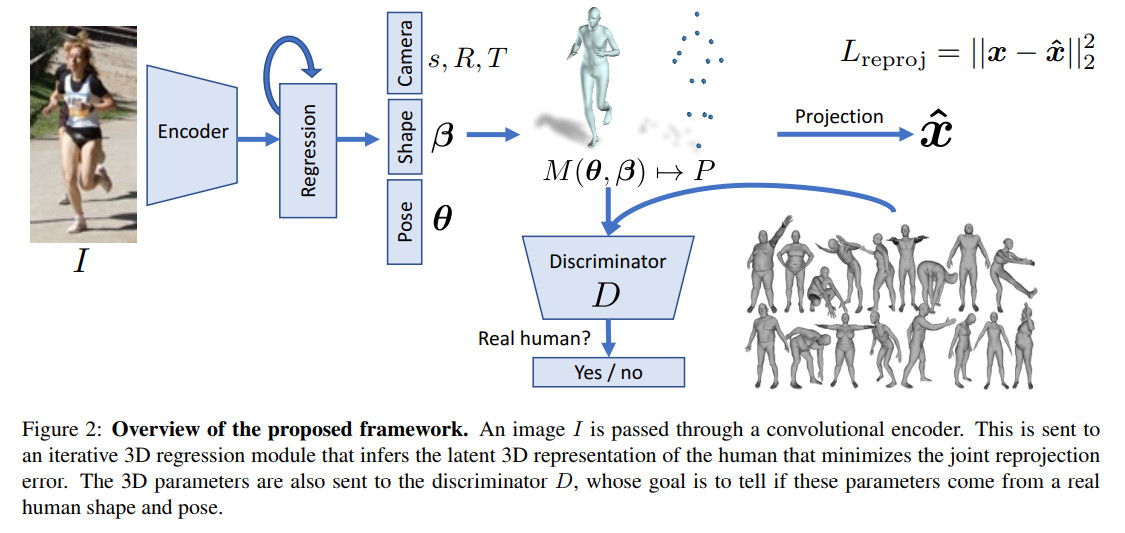
- Encoder和Regression
网络首先输入一张图片经过Encoder(Resnet-50)后,输出一个feature$\in \mathbb{R}^{2048}$。之后输入到一个Regressor(3层FC,2048D->1024D->1024D->85D)进行迭代,总共会迭代3次,每次迭代过程中会输入一个cam_para,shape $\beta$,pose $\theta$。将pose和shape输入smpl可以得到本次迭代后预测的模型(包括3D joint location)。由cam_para和3D joint location可以得到2D joint location从而可以计算$L_{reproj}$。由pose(也就是joint rotation)和shape可以计算出$L_{adv}$。若输入的2D image有对应的3D数据,则还可以计算$L_{3D}$。 但是在最后计算loss的时候,只会使用每次迭代时产生的$L_{adv}$,而$L_{3D}$和$L_{reproj}$只会利用最后一次迭代产生的loss。这是由于作者认为若每次迭代产生的loss全部都利用,这容易导致regressor限于局部最优化。
- Adversarial Prior
Adversarial Prior是用来解决上面提到的生成3D数据不真实情况的一个判别器。由于该判别器的任务是判断smpl参数是否是一个正常的人体,那么自然就不需要与输入2D image对应的3D ground truth数据来训练这个判别器判断参数的正确性。由于事先知道我们预测的latent space的意义,所以作者将整个discriminator分解为pose discriminator和shape discriminate。作者又进一步将pose discriminator分解为对每个关节点的判别器(23个,这些判别器的作用在于限制每个关节点的旋转角度)和一个对所有关节点整体做判断的判别器(这个判别器作用在于判断所有关节点的分布关系)。
作者认为因为这个网络结构不存在刻意去欺骗Discriminator的行为,所以不会产生一般GANs网络会产生的mode collapse现象。
- loss函数
$L = \lambda(L_{reproj} + \mathbb{1}L_{3D}) + L_{adv} $,$\lambda$是用来控制两个目标函数的相对权重的。若输入的2D图像有对应的ground truth 3D数据时,$\mathbb{1}$的值就为1,否则就是0。
$L_{reproj} = \sum \limits_{i}||v_{i}(x_{i}-\hat{x_{i}})||_{1}$,其中$\hat{x_{i}} = s\Pi(RX(\theta,\beta)) + t$。 $R$表示旋转操作,$\Pi$表示正交投影,$s,t$分别表示Scale和translation。
$L_{3D} = L_{3D joints} + L_{3D smpl}$
$L_{joints} = ||(X_i-\hat{X_i})||_2^2$
$L_{smpl} = ||[\beta_i,\theta_i]-[\hat{\beta_i},\hat{\theta_i}]||_2^2$
$minL_{abv}(E) = \sum_i\mathbb{E}_{\Theta ~ pE}[(D_i(E(I)-1)^2]$
$minL(D_i) = \mathbb{E}{\Theta~pdata}[(D_i(\Theta)-1)^2]+\mathbb{E}{\Theta ~ pE}[D_i(E(I)^2]$
很典型的GANs网络结构的Loss函数,其中$\Theta$表示真实的smpl参数。(这个loss函数真的能够限制每个关节的旋转角度和整体关节的分布情况么??表示很难理解,欢迎提出新的见解~)
Experiments
对于2D image dataset,作者使用了LSP,LSP-extended,MPII和MS COCO,训练数据量分别是1k,10k,20k和80k。2D image和3D dataset作者使用了Human 3.6M和MPI-INF-3DHP。而用作训练discriminator的SMPL真实数据是: CMU, Human3.6M training set 和the PosePrior dataset,训练数据量分别是390k,150k,180k。
作者在Human 3.6M上采用了两种评价标准:
- mean per joint position error (MPJPE)
- Reconstruction error, which is MPJPE after rigid alignment of the prediction with ground truth via Procrustes Analysis.
相较于第一种,Reconstruction error能排除全局误差的影响,更好的比较3D skeleton.
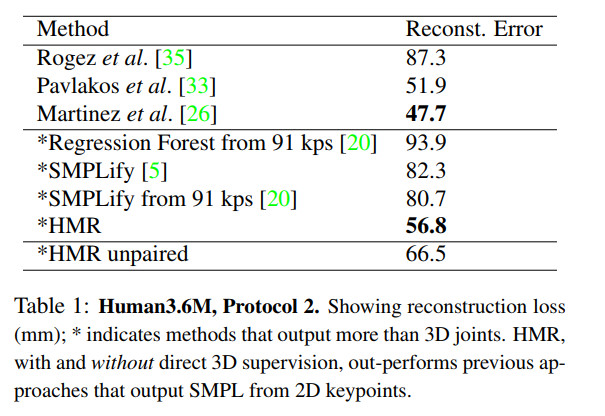
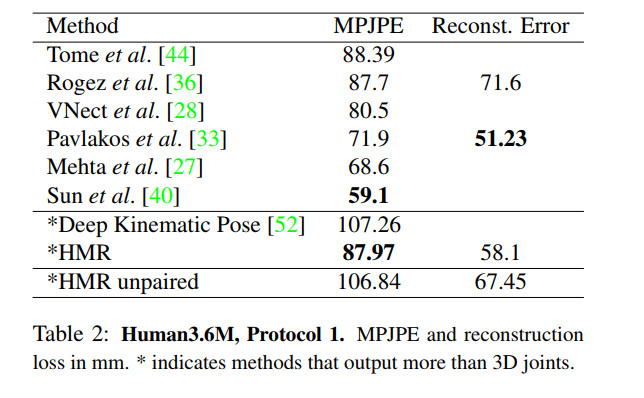
作者发现即使拥有较高的MPJPE,文中的方法生成的3D模型从视觉效果上看,也不错。
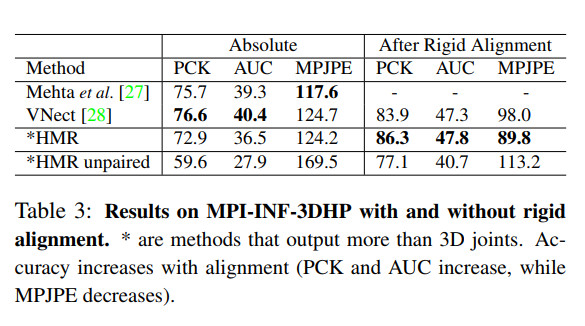
作者在MPI-INF-3DHP上采用了两种评价标准:
- Percentage of Correct Keypoints(PCK) thresholded at 150mm
- Area Under the Curve(AUC) over a range of PCK thresholds