<论文阅读>(一)Learning Category-Specific Mesh Reconstruction From Image Collections

<论文阅读>Learning Category-Specific Mesh Reconstruction from Image Collections

Contribution

单图重建
纹理渲染
训练过程无需3d ground truth数据

Method

训练数据预处理

本次实验用到的数据集是CUB-200-2011,提供了200种鸟类，共计11788张图片。每张图片附含了15个关键点的标记（头部，背部，脚等）、一张Mask和Bounding box。
作者首先将这些数据导入Matlab当中，首先对每组关键点进行零均值处理，接着计算平均模型$\hat{S}$。接着利用所有关键点进行structure from motion变换，得到每张图片相对于平均模型$\hat{S}$的rot,Translation和Scale三个参数。

网络训练

作者用到了三个网络来达到重建效果，分别是文中所用主体网络,Neural Mesh Render
和Perceptual loss。

论文中所用网络简介

首先网络接受一张图片，经过encoder之后变为了一个200d的shape feature f（注：encoder是一个经过imagenet预训练的resnet-18接上两个全连接层）。之后将得到的f送入三个网络,分别是ShapePredictor,CameraPredictor和UVMapPredictor. 其中ShapePredictor是预测形状变化$\Delta{V}$,最后的形状预测结果就是$V = \hat{V} + \Delta{V}$。CameraPredictor是预测rot,Translation和Scale三个参数的。值得一提的是rot参数,它与以前见到的旋转矩阵不同，rot$\in \mathbb{R}^4$,是一个四元数,可以用来表示三维空间中点的旋转。

TexturePredictor

作者提出的纹理预测思路比较巧妙。首先在数据预处理过程中的$\hat{S}$与网络训练过程的$\hat{V}$并不一致，实际上$\hat{V} =\mathcal{P}(\hat{S})$，$\mathcal{P}$表示将一个点数为642，面片数为1280的二十面体投影至$\hat{S}$。在将二十面体投影至$\hat{S}$前，作者对二十面体的点，面做了一次重新排序，使他们的顺序按照独立点，左侧点，右侧点排列。而投影操作$\mathcal{P}$作者在代码注释中写了这么一句话：

def triangle_direction_intersection(tri, trg):
    Finds where an origin-centered ray going in direction trg intersects a triangle.
    Args:
        tri: 3 X 3 vertex locations. tri[0, :] is 0th vertex.

多边形相当于二十面体，而中间的三角形就相当于$\hat{S}$,其边就可以看作三角面片。投影操作就是求解沿着二十面体点的方法，求与三角片面的交点。

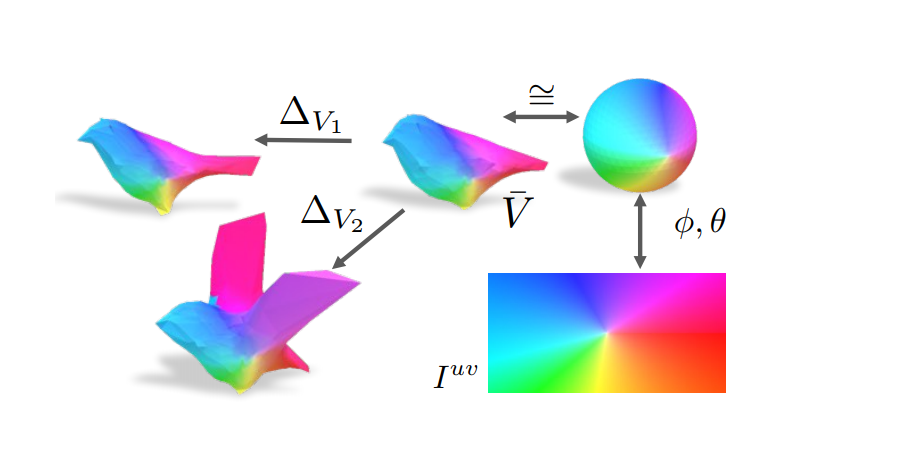
有了上面的基础，作者就认为由于所有的预测3D模型都是从同一个平均模型在保持拓扑变化的基础上变化得到的原因，所以每个所预测3D模型的点语义都是一致，即编号为1的点若代表嘴巴，则所有预测模型中编号为1的点就是所预测的嘴巴那个点。那么对于所预测的纹理图片来说，只要知道了最原始的那个二十面体的UV图，便可以对预测3D模型进行渲染(rendering)。

Loss函数介绍

** 注1：$\mathcal{R}$（）和$G$（）分别表示渲染(rendering)和双线性取样(bilinear sampling),其中$\mathcal{R}$（）引用自*Hiroharu Kato, etc. Neural 3D Mesh Renderer

** 注2：$L_{texture}$函数表示的percetual loss,较传统的pixel loss相比更能从人的感知角度来评价两幅图像的相似度引用自**Zhang,R etc. The unreasonable effectiveness of deep networks as a perceptual metric. In CVPR 2018

$L_1 = L_{reproj} + L_{mask} + L_{cam} + L_{smooth} + L_{def} + L_{vert2kp}$

$L_{reproj} = \sum_{i}^{}||x_{i}-\tilde{\pi}_{i}(AV_{i})||_{2}$，其中 $\tilde{\pi}（*）$表示投影操作，其值是从structure-from-motion中获得参数

$L_{mask} = \sum_i||S_{i}-\mathcal{R}(V_{i},F,\tilde{\pi}_{i})||_{2}$，$S_{i}$表示ground-truth的Mask。

$L_{cam} = \sum_{i}||\tilde{\pi}_{i}-{\pi}_{i}||_{2}$，$\pi_{i}$表示估计的相机旋转参数，由于旋转参数是由四元数表示，那么就是利用hamilton_product来求解估计与实际的误差

$L_{smooth} = ||LV||_{2}$，$L$表示Laplacian光滑，其目的是为了最小化平均曲率

$L_{def}=||\Delta{V}||_{2}$，这个是一个正则项

$L_{vert2kp} = \frac{1}{|K|}\sum_{k}\sum_{v}-A_{k,v}logA_{k,v}$，这个是一个k*V的矩阵，每一行表示一个特征点，而每一列表示这个特征点在各个点的概率分布。初始化是，每个特征点在各个点上的概率分布是一致的，进过迭代之后，作者期望形成一个类似与one-hot的矩阵。

$L_2 = L_{texture} + L_{dt}$

$L_{texture} = \sum_{i}dist(\mathcal{S_{i}}\bigodot\mathcal{I_{i}},\mathcal{S_{i}}\bigodot\mathcal{R}(V_{i},F,\tilde{\pi_{i}},I^{uv}))$

$L_{dt} = \sum_{i}\sum_{u,v}G(\mathcal{D_{S_{i}};F_{i}}(u,v)$， $\mathcal{D_{S_{i}}}$表示对于每一个Mask的distance transform。

TexturePredictor会输出一个texture flow，也就是$\mathcal{F} \in \mathbb{R}^{H_{uv} * W_{uv} * 2}$,其中$H_{uv}*W_{uv}$分别表示UVmap的长和宽，而$\mathcal{F}(x,y)$对应的就是input image(x,y)。最后的UVmap就是$I^{uv} = G(I;\mathcal{F})$。而这个texture flow不是神经网络的直接输出产物，而神经网络直接输出的是一个表示体现了UV图和Img的对应位置的关系，而其还是会与另一个UVsample进行取样。而UVsample表示的是UV图与$\hat{V}$上各个点的一个对应关系。这两个东西结合在一起后就可以体现UVmap、$\hat{V}$、img三者之间的关系。

Diver